hubungan pola alam dan matematika (bilangan fibonacci)

Matematika...

Apa yang anda pikirkan setelah mendengar kata ini?

Kebanyakan orang mendengar kata ini akan teringat ”sesuatu yang rumit, rumus, membosankan bahkan menyebalkan” bahkan pernah seorang teman saya berkomentar ”matematika itu sebatas, kertas, pensil, dan rumus yang rumit”, padahal matematika itu sesuatu yang unik, bahkan banyak pola kehidupan yang tak jauh dari matematika.

1 contoh yang cukup unik adalah deret fibonacci, apa itu deret fibonacci dan hubungannya dengan pola di alam sekitar kita??

Cekkiddoott  :D

Sedikit  mengulas sejarah fibonancci:

Deret Fibonacci ditemukan oleh Leonardi Pisano atau lebih dikenal dengan sebutan Leonardo Fibonacci (diturunkan dari Filius Bonaccio atau anak dari Bonaccio, sebutan bagi ayahnya yang bernama asli Guglielmo), pada abad 12 di Italia. Pada dasarnya deret fibonacci merupakan barisan bilangan sederhana dimulai dari 0 dan 1 dan suku berikutnya merupakan jumlah dua bilangan sebelumnya. Deret fibonacci bersifat rekursif karena menggunakan suku dalam deret tersebut untuk menghitung suku setelahnya. Dengan pengertian tersebut, maka suku-suku pada deret fibonacci adalah:
 0 1 1 2 3 5 8 13 21 34 55 89 144 233, 377, 610, 987, 1597, 2584, 4181, dan seterusnya.

Rumus pola bilangan fibonacci adalah:

      Dalam deret bilangan fibonacci, rasio dari sepasang suku berurutan akan konvergen ke sebuah bilangan irasional 1,618 atau bilangan phi (Φ). Phi, merupakan sebuah konstanta irasional yang bernilai 1,61803399… yang di dapat dari kenvergensi rasio suku dalam deret fibonacci terhadap suku sbelumnya.
Fakta-Fakta Bilangan Fibonacci
1. Cangkang keong
Rasio Fibonacci banyak terdapat pada benda-benda di alam ini dan beberapa karya manusia. Contohnya pola pada cangkang keong seperti pada gambar di bawah ini.

2. Jumlah Daun pada Bunga (petals)
Mungkin sebagian besar tidak terlalu memperhatikan jumlah daun pada sebuah bunga. Dan bila diamati, ternyata jumlah daun pada bunga itu menganut deret fibonacci. contohnya:

•  jumlah daun bunga 3 : bunga lili, iris
•  jumlah daun bunga 5 : buttercup (sejenis bunga mangkok)
•  jumlah daun bunga 13 : ragwort, corn marigold, cineraria,
•  jumlah daun bunga 21 : aster, black-eyed susan, chicory
•  jumlah daun bunga 34 : plantain, pyrethrum
•  jumlah daun bunga 55,89 : michaelmas daisies, the asteraceae family

Ingin lihat buktinya? silahkan diamati beberapa gambar berikut :

2. Pola Bunga
Pola bunga juga menunjukkan adanya pola fibonacci ini, misalnya pada bunga matahari.

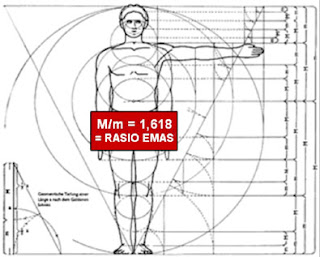
3. Tubuh Manusia
Hubungan kesesuaian “ideal” yang dikemukakan ada pada berbagai bagian tubuh manusia rata-rata dan yang mendekati nilai rasio emas dapat dijelaskan dalam sebuah bagan umum sebagaimana berikut:Nilai perbandingan M/m pada diagram berikut selalu setara dengan rasio emas. M/m = 1,618

Contoh pertama dari rasio emas pada tubuh manusia rata-rata adalah jika antara pusar dan telapak kaki dianggap berjarak 1 unit, maka tinggi seorang manusia setara dengan 1,618 unit. Beberapa rasio emas lain pada tubuh manusia rata-rata adalah:

• Jarak antara ujung jari dan siku / jarak antara pergelangan tangan dan siku,
• Jarak antara garis bahu dan unjung atas kepala / panjang kepala,
• Jarak antara pusar dan ujung atas kepala / jarak antara garis bahu dan ujung atas kepala,
• Jarak antara pusar dan lutut / jarak antara lutut dan telapak kaki.

4. Daun, tangkai, serangga, dan semua yang berbentuk spiral, bila dibandingkan antara panjang spiral terakhir dengan sebelumnya, maka hasilnya akan selalu 1.618.

5. Kabarnya, Stradivarius, pencipta bola, juga menggunakan angka ini dalam peletakan lubang di bola.

6. Parthenon

Bangunan yang diarsiteki oleh Phidias ini juga menggunakan perbandingan yang berdasarkan angka Phi. 1.618.

7. Perkembangbiakan sepasang kelinci
Menurut, sebuah penelitian yang dilakukan, sepasang Kelinci berkembang biak dengan pola deret angka Fibonacci ini.

Bahkan sedikit tambahan, ”kemenangan obama sebagai Periden Amerika Serikat”

Topik ini hanyalah sebuah tambahan saja. Ada sebuah penelitian yang dipublikasikan pada bulan Juni 2008, pada saat itu masih dalam tahap kampanye calon Presiden Obama dan MacCain, yang mana penelitian tersebut mengemukakan dan
tepatnya mungkin meramalkan bahwa Obama akan menjadi Presiden Amerika yang ke-44.

Penelitian ini didasarkan pada kejadian-kejadian politik di Amerika yang ada kaitannya dengan kehidupan politik orang kulit hitam di Amerika (African-Americans). Pada penelitian itu disebutkan bahwa berdasarkan deret tahun kejadian politik di Amerika, maka Obama memiliki peluang yang besar untuk menjadi Presiden Amerika.

Nah, ternyata kenyataannya itu terbukti.

Jadi, jika beberapa orang berpendapat matematikaa hanya  membuat pusing dan kurang teraplikasi dalam kehidupan sehari hari, itu adalah salah :)

Trimakasih sudah menyempatkan sedikit waktunya tuk membaca :)